Which Energy Changes Are Associated With A Liquid Freezing?
11.4: Stage Changes
- Folio ID
- 21772
Learning Objectives
- To summate the energy changes that accompany phase changes.
We take advantage of changes between the gas, liquid, and solid states to cool a drink with water ice cubes (solid to liquid), cool our bodies past perspiration (liquid to gas), and cool food within a refrigerator (gas to liquid and vice versa). We use dry ice, which is solid CO2, equally a refrigerant (solid to gas), and we brand artificial snow for skiing and snowboarding by transforming a liquid to a solid. In this section, we examine what happens when whatever of the 3 forms of matter is converted to either of the other two. These changes of state are frequently called phase changes. The six most common phase changes are shown in Figure \(\PageIndex{1}\).
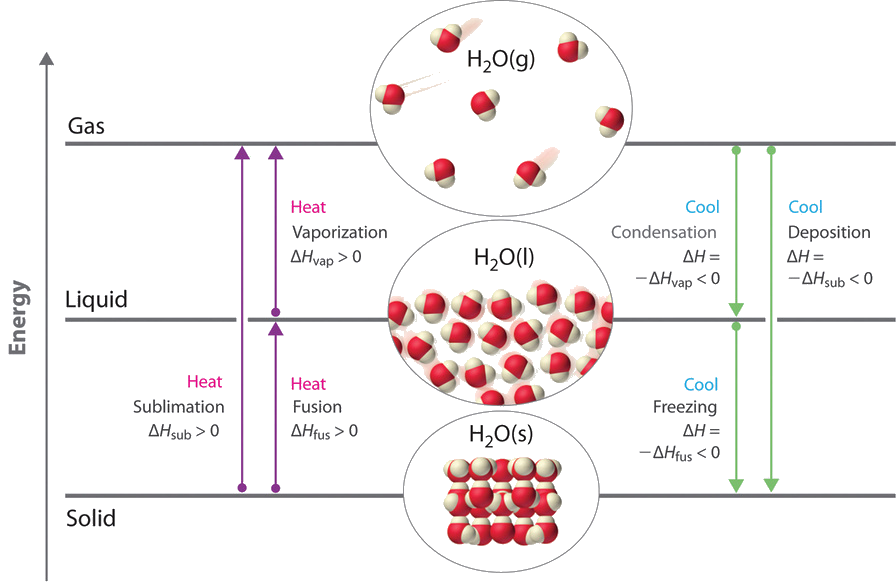
Energy Changes That Accompany Phase Changes
Phase changes are always accompanied by a change in the energy of a organisation. For case, converting a liquid, in which the molecules are close together, to a gas, in which the molecules are, on average, far autonomously, requires an input of energy (heat) to give the molecules enough kinetic energy to permit them to overcome the intermolecular bonny forces. The stronger the bonny forces, the more than energy is needed to overcome them. Solids, which are highly ordered, accept the strongest intermolecular interactions, whereas gases, which are very disordered, have the weakest. Thus whatsoever transition from a more ordered to a less ordered state (solid to liquid, liquid to gas, or solid to gas) requires an input of energy; it is endothermic. Conversely, whatsoever transition from a less ordered to a more ordered state (liquid to solid, gas to liquid, or gas to solid) releases free energy; information technology is exothermic. The energy modify associated with each common stage alter is shown in Figure \(\PageIndex{1}\).
ΔH is positive for whatever transition from a more ordered to a less ordered state and negative for a transition from a less ordered to a more than ordered state.
Previously, we defined the enthalpy changes associated with various chemical and physical processes. The melting points and molar enthalpies of fusion (\(ΔH_{fus}\)), the energy required to convert from a solid to a liquid, a process known every bit fusion (or melting), every bit well every bit the normal boiling points and enthalpies of vaporization (\(ΔH_{vap}\)) of selected compounds are listed in Table \(\PageIndex{1}\).
| Substance | Melting Point (°C) | ΔHfus (kJ/mol) | Humid Point (°C) | ΔHvap (kJ/mol) |
|---|---|---|---|---|
| N2 | −210.0 | 0.71 | −195.8 | 5.6 |
| HCl | −114.ii | 2.00 | −85.1 | 16.ii |
| Brtwo | −7.2 | 10.6 | 58.eight | 30.0 |
| CCl4 | −22.6 | 2.56 | 76.viii | 29.eight |
| CHiiiCH2OH (ethanol) | −114.1 | 4.93 | 78.3 | 38.six |
| CH3(CH2)fourCHiii (n-hexane) | −95.4 | 13.ane | 68.7 | 28.ix |
| H2O | 0 | six.01 | 100 | 40.7 |
| Na | 97.8 | 2.6 | 883 | 97.4 |
| NaF | 996 | 33.iv | 1704 | 176.i |
The substances with the highest melting points usually have the highest enthalpies of fusion; they tend to be ionic compounds that are held together by very stiff electrostatic interactions. Substances with high humid points are those with potent intermolecular interactions that must be overcome to convert a liquid to a gas, resulting in loftier enthalpies of vaporization. The enthalpy of vaporization of a given substance is much greater than its enthalpy of fusion because information technology takes more free energy to completely separate molecules (conversion from a liquid to a gas) than to enable them just to move by one another freely (conversion from a solid to a liquid).
Less energy is needed to allow molecules to move past each other than to divide them totally.
The direct conversion of a solid to a gas, without an intervening liquid stage, is called sublimation. The amount of free energy required to sublime 1 mol of a pure solid is the enthalpy of sublimation (ΔH sub). Mutual substances that sublime at standard temperature and pressure (STP; 0°C, 1 atm) include COii (dry out ice); iodine (Figure \(\PageIndex{two}\)); naphthalene, a substance used to protect woolen clothing against moths; and i,4-dichlorobenzene. As shown in Figure \(\PageIndex{1}\), the enthalpy of sublimation of a substance is the sum of its enthalpies of fusion and vaporization provided all values are at the same T; this is an application of Hess'southward police.
\[ΔH_{sub} =ΔH_{fus} +ΔH_{vap} \label{Eq1}\]
Fusion, vaporization, and sublimation are endothermic processes; they occur but with the absorption of heat. Anyone who has ever stepped out of a swimming pool on a absurd, breezy twenty-four hour period has felt the oestrus loss that accompanies the evaporation of h2o from the skin. Our bodies use this same phenomenon to maintain a constant temperature: nosotros perspire continuously, fifty-fifty when at rest, losing virtually 600 mL of h2o daily by evaporation from the skin. We also lose about 400 mL of water every bit water vapor in the air we exhale, which as well contributes to cooling. Refrigerators and air-conditioners operate on a similar principle: heat is captivated from the object or expanse to be cooled and used to vaporize a low-boiling-betoken liquid, such as ammonia or the chlorofluorocarbons (CFCs) and the hydrofluorocarbons (HCFCs). The vapor is and so transported to a unlike location and compressed, thus releasing and dissipating the heat. Likewise, ice cubes efficiently cool a drinkable not because of their depression temperature simply considering oestrus is required to convert ice at 0°C to liquid h2o at 0°C.
Temperature Curves
The processes on the right side of Figure \(\PageIndex{1}\)—freezing, condensation, and deposition, which are the opposite of fusion, sublimation, and vaporization—are exothermic. Thus rut pumps that utilize refrigerants are essentially air-conditioners running in opposite. Heat from the environment is used to vaporize the refrigerant, which is so condensed to a liquid in coils within a house to provide heat. The energy changes that occur during phase changes tin can be quantified by using a heating or cooling curve.
Heating Curves
Figure \(\PageIndex{3}\) shows a heating curve, a plot of temperature versus heating time, for a 75 thousand sample of h2o. The sample is initially ice at 1 atm and −23°C; as heat is added, the temperature of the ice increases linearly with fourth dimension. The slope of the line depends on both the mass of the ice and the specific heat (C s) of ice, which is the number of joules required to raise the temperature of one yard of water ice by 1°C. As the temperature of the ice increases, the water molecules in the ice crystal absorb more and more free energy and vibrate more than vigorously. At the melting point, they take enough kinetic energy to overcome bonny forces and move with respect to one another. As more heat is added, the temperature of the system does non increment further simply remains constant at 0°C until all the water ice has melted. Once all the ice has been converted to liquid water, the temperature of the water again begins to increase. Now, withal, the temperature increases more slowly than before because the specific heat capacity of h2o is greater than that of water ice. When the temperature of the water reaches 100°C, the water begins to boil. Here, also, the temperature remains constant at 100°C until all the water has been converted to steam. At this bespeak, the temperature again begins to rise, simply at a faster charge per unit than seen in the other phases considering the estrus chapters of steam is less than that of water ice or water.
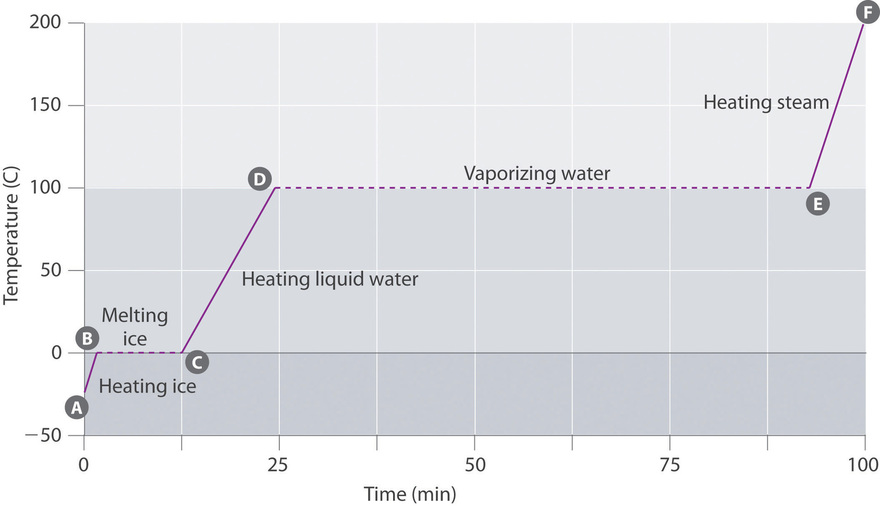
Thus the temperature of a system does not change during a phase modify. In this example, as long equally fifty-fifty a tiny amount of ice is present, the temperature of the system remains at 0°C during the melting process, and equally long as fifty-fifty a small amount of liquid water is present, the temperature of the organization remains at 100°C during the humid procedure. The rate at which heat is added does not impact the temperature of the ice/water or water/steam mixture considering the added heat is being used exclusively to overcome the bonny forces that hold the more condensed phase together. Many cooks recollect that food will cook faster if the heat is turned up college so that the water boils more rapidly. Instead, the pot of h2o volition eddy to dryness sooner, but the temperature of the water does not depend on how vigorously information technology boils.
The temperature of a sample does not change during a phase modify.
If heat is added at a abiding charge per unit, as in Figure \(\PageIndex{3}\), and then the length of the horizontal lines, which represents the time during which the temperature does not alter, is directly proportional to the magnitude of the enthalpies associated with the phase changes. In Figure \(\PageIndex{3}\), the horizontal line at 100°C is much longer than the line at 0°C because the enthalpy of vaporization of water is several times greater than the enthalpy of fusion.
A superheated liquid is a sample of a liquid at the temperature and pressure at which information technology should be a gas. Superheated liquids are not stable; the liquid will eventually boil, sometimes violently. The phenomenon of superheating causes "bumping" when a liquid is heated in the laboratory. When a test tube containing water is heated over a Bunsen burner, for example, one portion of the liquid can easily become too hot. When the superheated liquid converts to a gas, it can push or "bump" the residue of the liquid out of the test tube. Placing a stirring rod or a modest slice of ceramic (a "boiling chip") in the test tube allows bubbling of vapor to form on the surface of the object so the liquid boils instead of becoming superheated. Superheating is the reason a liquid heated in a smoothen cup in a microwave oven may not eddy until the loving cup is moved, when the motion of the cup allows bubbles to form.
Cooling Curves
The cooling curve, a plot of temperature versus cooling time, in Figure \(\PageIndex{4}\) plots temperature versus time every bit a 75 g sample of steam, initially at ane atm and 200°C, is cooled. Although we might expect the cooling bend to be the mirror image of the heating bend in Effigy \(\PageIndex{3}\), the cooling curve is non an identical mirror prototype. Equally oestrus is removed from the steam, the temperature falls until it reaches 100°C. At this temperature, the steam begins to condense to liquid water. No farther temperature change occurs until all the steam is converted to the liquid; and then the temperature again decreases every bit the water is cooled. We might expect to achieve another plateau at 0°C, where the water is converted to ice; in reality, withal, this does not always occur. Instead, the temperature often drops below the freezing bespeak for some time, as shown by the niggling dip in the cooling bend below 0°C. This region corresponds to an unstable class of the liquid, a supercooled liquid. If the liquid is allowed to stand, if cooling is continued, or if a small crystal of the solid phase is added (a seed crystal), the supercooled liquid will convert to a solid, sometimes quite of a sudden. As the water freezes, the temperature increases slightly due to the heat evolved during the freezing process and and then holds constant at the melting indicate equally the balance of the water freezes. Subsequently, the temperature of the water ice decreases once more as more heat is removed from the arrangement.
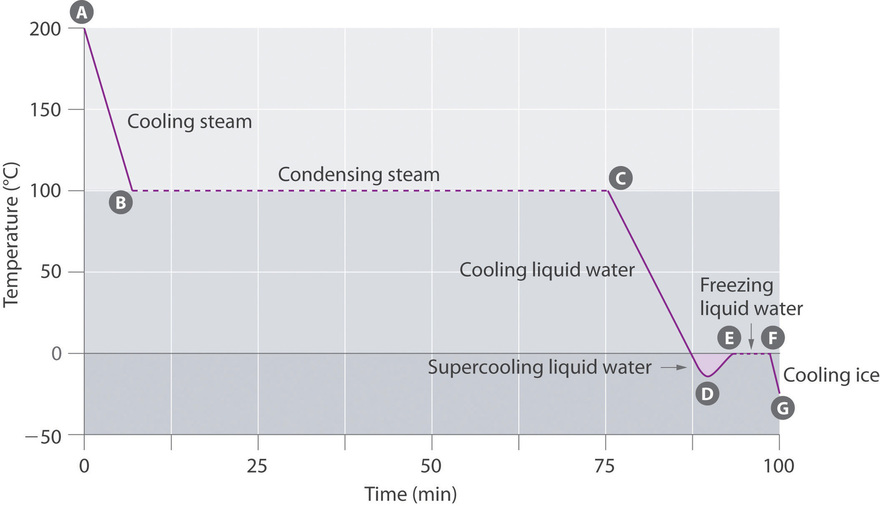
Supercooling furnishings have a huge impact on Earth'southward climate. For example, supercooling of h2o aerosol in clouds can prevent the clouds from releasing precipitation over regions that are persistently arid every bit a result. Clouds consist of tiny droplets of water, which in principle should exist dumbo plenty to fall as pelting. In fact, however, the aerosol must aggregate to reach a sure size before they can fall to the ground. Usually a small particle (a nucleus) is required for the droplets to amass; the nucleus can be a dust particle, an water ice crystal, or a particle of silver iodide dispersed in a cloud during seeding (a method of inducing rain). Unfortunately, the small droplets of water generally remain as a supercooled liquid downwardly to nearly −10°C, rather than freezing into ice crystals that are more suitable nuclei for raindrop formation. 1 arroyo to producing rainfall from an existing deject is to cool the h2o droplets so that they crystallize to provide nuclei around which raindrops can abound. This is best done by dispersing pocket-size granules of solid CO2 (dry ice) into the deject from an aeroplane. Solid CO2 sublimes direct to the gas at pressures of 1 atm or lower, and the enthalpy of sublimation is substantial (25.3 kJ/mol). Equally the CO2 sublimes, it absorbs heat from the cloud, frequently with the desired results.
A Video Discussing the Thermodynamics of Phase Changes. Video Source: https://youtu.be/Uf2mAuP1BZY
Case \(\PageIndex{1}\): Cooling Tea
If a l.0 thou ice cube at 0.0°C is added to 500 mL of tea at 20.0°C, what is the temperature of the tea when the ice cube has just melted? Assume that no heat is transferred to or from the surroundings. The density of h2o (and iced tea) is 1.00 1000/mL over the range 0°C–20°C, the specific heats of liquid water and ice are 4.184 J/(thousand•°C) and two.062 J/(g•°C), respectively, and the enthalpy of fusion of ice is 6.01 kJ/mol.
Given: mass, volume, initial temperature, density, specific heats, and \(ΔH_{fus}\)
Asked for: final temperature
Strategy
Substitute the given values into the general equation relating rut gained (past the ice) to heat lost (past the tea) to obtain the final temperature of the mixture.
Solution
When two substances or objects at different temperatures are brought into contact, heat will period from the warmer 1 to the libation. The corporeality of heat that flows is given by
\[q=mC_sΔT \nonumber\]
where \(q\) is heat, \(m\) is mass, \(C_s\) is the specific rut, and \(ΔT\) is the temperature alter. Somewhen, the temperatures of the two substances will get equal at a value somewhere betwixt their initial temperatures. Calculating the temperature of iced tea after calculation an water ice cube is slightly more complicated. The full general equation relating heat gained and rut lost is nevertheless valid, but in this case we too accept to have into account the amount of heat required to cook the ice cube from ice at 0.0°C to liquid water at 0.0°C.
The amount of heat gained by the ice cube as it melts is adamant by its enthalpy of fusion in kJ/mol:
\[q=nΔH_{fus} \nonumber\]
For our 50.0 yard ice cube:
\[\brainstorm{align*} q_{ice} &= 50.0 g⋅\dfrac{ane\: mol}{18.02\:g}⋅6.01\: kJ/mol \\[4pt] &= sixteen.7\, kJ \cease{marshal*}\]
Thus, when the ice cube has just melted, it has absorbed 16.seven kJ of heat from the tea. We can and so substitute this value into the beginning equation to make up one's mind the change in temperature of the tea:
\[q_{tea} = - 16,700 J = 500 mL⋅\dfrac{1.00\: m}{i\: mL}⋅iv.184 J/(g•°C) ΔT \nonumber\]
\[ΔT = - 7.98 °C = T_f - T_i \]
\[T_f = 12.02 °C \]
This would be the temperature of the tea when the ice cube has just finished melting; even so, this leaves the melted ice still at 0.0°C. Nosotros might more practically want to know what the terminal temperature of the mixture of tea will be once the melted ice has come to thermal equilibrium with the tea. To make up one's mind this, we tin add ane more step to the calculation by plugging in to the full general equation relating heat gained and heat lost again:
\[\begin{align*} q_{ice} &= - q_{tea} \\[4pt] q_{ice} &= m_{water ice}C_sΔT = 50.0g⋅iv.184 J/(m•°C)⋅(T_f - 0.0°C) \\[4pt] &= 209.2 J/°C⋅T_f \end{align*}\]
\[q_{tea} = m_{tea}C_sΔT = 500g⋅4.184 J/(g•°C)⋅(T_f - 12.02°C) = 2092 J/°C⋅T_f - 25,150 J \]
\[209.two J/°C⋅T_f = - 2092 J/°C⋅T_f + 25,150 J \]
\[2301.two J/°C⋅T_f = 25,150 J \]
\[T_f = 10.ix °C \]
The final temperature is in betwixt the initial temperatures of the tea (12.02 °C) and the melted ice (0.0 °C), so this respond makes sense. In this case, the tea loses much more than heat in melting the ice than in mixing with the common cold water, showing the importance of accounting for the oestrus of phase changes!
Practice \(\PageIndex{1}\): Expiry past Freezing
Suppose you are overtaken past a blizzard while ski touring and you have refuge in a tent. You lot are thirsty, but you lot forgot to bring liquid water. You take a choice of eating a few handfuls of snowfall (say 400 grand) at −5.0°C immediately to quench your thirst or setting upward your propane stove, melting the snowfall, and heating the water to body temperature before drinking it. You recall that the survival guide you leafed through at the hotel said something about not eating snow, merely you lot cannot think why—after all, it's just frozen water. To understand the guide's recommendation, calculate the amount of heat that your torso will have to supply to bring 400 g of snow at −five.0°C to your body'due south internal temperature of 37°C. Use the data in Example \(\PageIndex{ane}\)
- Answer
-
200 kJ (four.ane kJ to bring the ice from −5.0°C to 0.0°C, 133.6 kJ to melt the ice at 0.0°C, and 61.ix kJ to bring the water from 0.0°C to 37°C), which is free energy that would not have been expended had you first melted the snowfall.
Summary
Fusion, vaporization, and sublimation are endothermic processes, whereas freezing, condensation, and deposition are exothermic processes. Changes of country are examples of phase changes, or phase transitions. All stage changes are accompanied by changes in the free energy of a organization. Changes from a more-ordered state to a less-ordered land (such as a liquid to a gas) are endothermic. Changes from a less-ordered land to a more-ordered state (such as a liquid to a solid) are always exothermic. The conversion of a solid to a liquid is called fusion (or melting). The energy required to cook one mol of a substance is its enthalpy of fusion (ΔH fus). The energy change required to vaporize 1 mol of a substance is the enthalpy of vaporization (ΔH vap). The direct conversion of a solid to a gas is sublimation. The amount of energy needed to sublime 1 mol of a substance is its enthalpy of sublimation (ΔH sub) and is the sum of the enthalpies of fusion and vaporization. Plots of the temperature of a substance versus heat added or versus heating fourth dimension at a constant rate of heating are called heating curves. Heating curves chronicle temperature changes to phase transitions. A superheated liquid, a liquid at a temperature and pressure at which information technology should be a gas, is non stable. A cooling curve is not exactly the reverse of the heating curve because many liquids exercise not freeze at the expected temperature. Instead, they form a supercooled liquid, a metastable liquid phase that exists below the normal melting indicate. Supercooled liquids normally crystallize on standing, or adding a seed crystal of the same or some other substance can induce crystallization.
Source: https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_Chemistry_-_The_Central_Science_(Brown_et_al.)/11%3A_Liquids_and_Intermolecular_Forces/11.04%3A_Phase_Changes
Posted by: desrochersponoulace.blogspot.com

0 Response to "Which Energy Changes Are Associated With A Liquid Freezing?"
Post a Comment